讲解神经网络训练难得原因,提出Xavier权重初始化方法
概要
神经网络难以训练,作者想要读者更好理解:为什么梯度下降法不适用随机初始化权重的神经网络,且怎么设计更好的初始化方法。
作者发现随机化初始化权重时,不适合使用sigmod作为激活函数,因为它均值不为零,前面的hidden layer容易饱和;令人惊讶的时饱和的神经元可以自动变为不饱和,尽管过程很慢。
作者通过观察不同层的激活函数和梯度,提出了新的权重初始化方法,可以更快的是网络收敛。
Sigmod实验
bias初始化为零,权重初始化
$$ W_{ij} \sim U[-\frac{1}{\sqrt n},\frac{1}{\sqrt n}] $$$n$表示前一层的size(即前一层权重W的列数)
下图是5层网络中,4个隐藏层的激活值随epoc的变化:
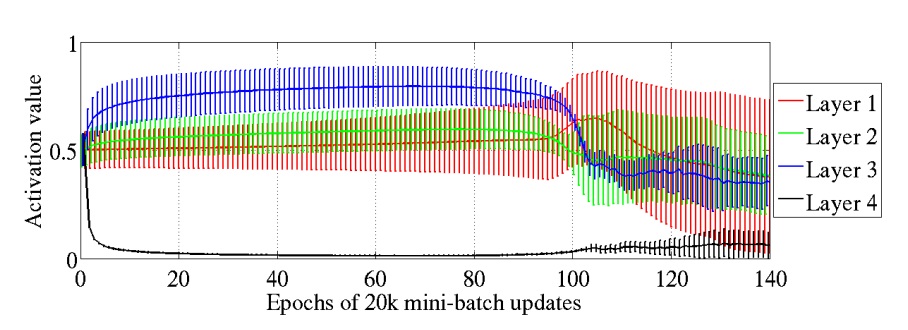
通过图片可以看到,最后的隐藏层很快饱和,但是在epoch 100左右,又开始变为不饱和。其它几层的均值大概为0.5,随着训练进行开始变小。
上面这种情况很可能是因为随机初始化权重引起的。输出层为$softmax(b+Wh)$,这样的话,输出的结果更加依赖$b$(因为h饱和,接近为0),bias学习速度将会比$h$快。梯度误差将会使$Wh$向零靠近,造成前面的层学习不到有用的特征。这样训练的网络质量差,泛化性能差。
作者还对比了使用不同激活函数的情况。
代价函数的影响
在逻辑回归或似然估计时,使用softmax输出,cost function为对数函数$-logP(y|x)$比二次代价函数要好。一个2层网络,代价函数随两层网络权重变化如图:
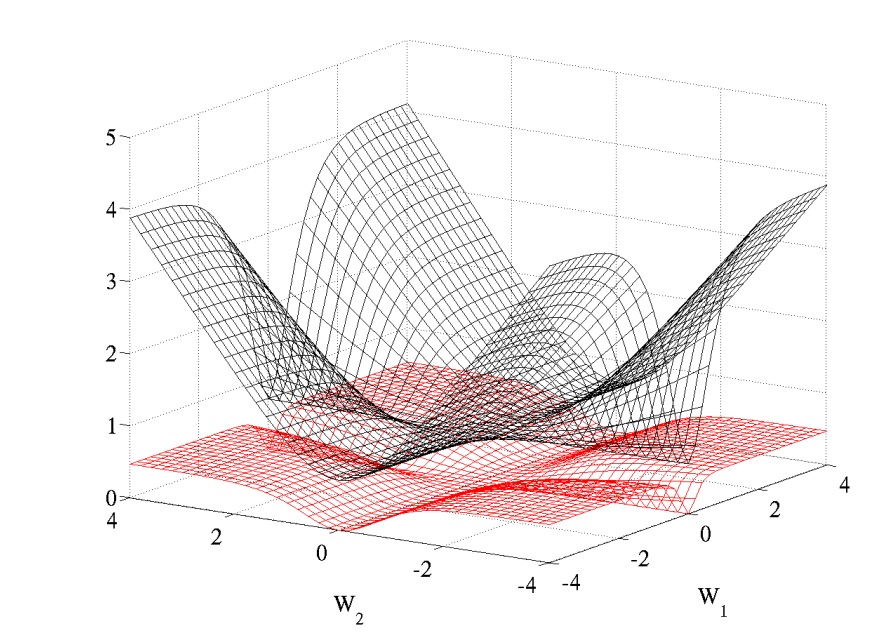
交叉熵代价函数是黑色,二次型代价函数是红色;$W_1$和$W_2$分别表示两层的权重。可以看出二次型代价函数有明显的“平”的区域。
权重初始化
为了便于研究,假设使用线性激活函数$f(x)$,且在零点导数$f’(x)=1$。
对于一层网络
$$ f(\textbf x) = \sum_i^n w_ix_i + b $$输出的方差
$$
Var(f(\textbf x)) = \sum_i^n Var(w_i x_i)
$$
其中
$$
Var(w_i x_i) = E[w_i]^2Var(x_i) + E[x_i]^2Var(w_i)+Var(w_i)Var(x_i)\\
因为:E[x_i] = E[w_i] = 0\\
Var(w_i x_i) =Var(w_i)Var(x_i)
$$
由于$w$和$x$独立同分布
$$
Var(f(\textbf x)) = n Var(w_i) Var(x_i)
$$
假设$\textbf z^i$是第$i$层的输入向量,$\textbf s^i$是第$i$层激活函数的输入
$$ \textbf s^i = \textbf z^i W^i + \textbf b^i \\ \textbf z^{i+1} = f(\textbf s^i) $$可以得到
$$
\frac{\partial Cost}{\partial s_k^i} = f'(s_k^i) W_{k,\cdot}^{i+1} \frac{\partial Cost}{\partial s^{i+1}} \\
\frac{\partial Cost}{\partial w_{l,k}^i} = z_l^i \frac{\partial Cost}{\partial s_k^i}
$$
假设第$i$层的大小为$n_i$,网络输入为$x$
$$ f'(s_k^i) \approx 1\\ Var[z^i] = Var[x] \prod_{i'=0}^{i-1}n_{i'} Var[W^{i'}] $$其中$Var[W^{i’}]$表示第$i’$层的共享权重的方差,对于$d$层的网络
$$
Var[\frac{\partial Cost}{\partial s^i}]=Var[\frac{\partial Cost}{\partial s^d}] \prod_{i'=i}^{d}n_{i'+1} Var[W^{i'}]
\\
Var[\frac{\partial Cost}{\partial w^i}]= \prod_{i'=0}^{i-1}n_{i'} Var[W^{i'}] \prod_{i'=i}^{d-1}n_{i'+1} Var[W^{i'}] \times Var[x] Var[\frac{\partial Cost}{\partial s^d}]
$$
对于前向传播
$$
\forall (i,i'), Var[z^i] = Var[z^{i'}]
$$
对于反向传播:
$$
\forall (i,i'), Var[\frac{\partial Cost}{\partial s^i}] = Var[\frac{\partial Cost}{\partial s^{i'}}]
$$
因此得到:
$$
\forall i, \quad n_i Var[W^i] = 1\\
\forall i, \quad n_{i+1} Var[W^i] = 1
$$
一个层的输入输出一般不相同,作为折中
$$
\forall i, \quad Var[W^i] = \frac{2}{n_i + n_{i+1}}
$$
对于
$$
W \sim U[-\frac{1}{\sqrt n},\frac{1}{\sqrt n}] \\
Var(W) = \frac{1}{3n}
$$
因此得到初始化权重:
$$
W \sim U[-\frac{\sqrt 6}{\sqrt {n_j + n_{j+1}}},\frac{\sqrt 6}{\sqrt {n_j + n_{j+1}}}]
$$